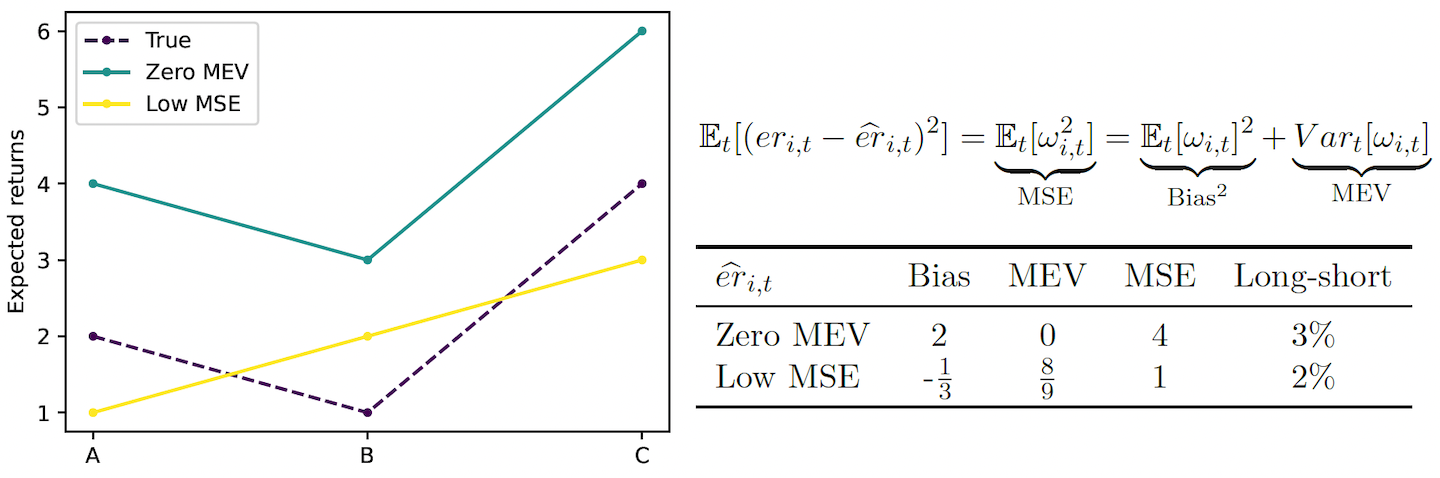
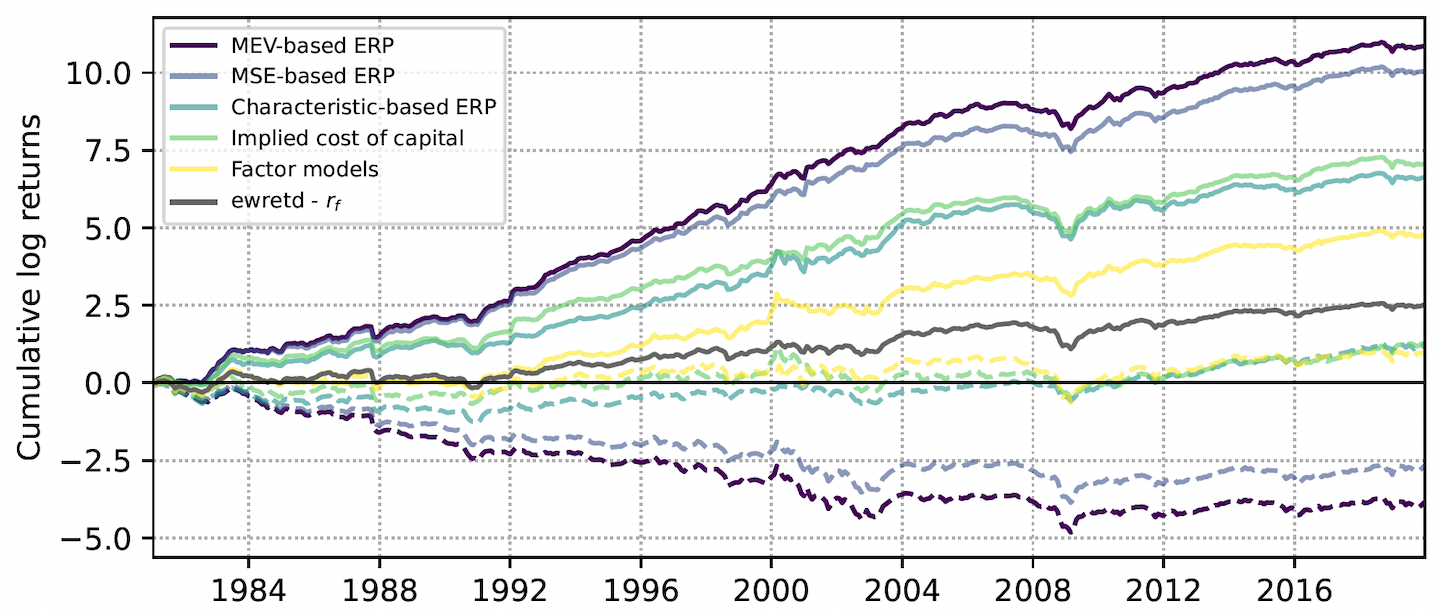
Abstract
I develop and test a new machine learning method for estimating cross-sectional firm-level expected returns. My approach adapts the loss function of a random forest algorithm to minimize the variance of measurement errors instead of trading off bias and variance. It yields higher cross-sectional accuracy out-of-sample than alternative estimates. I find that expected returns and the firm characteristics that explain them vary substantially across holding horizons. Applying this new approach, I show that cross-sectional differences in expected returns are larger and persist longer than previously documented, and I overturn prior results on the association between earnings smoothness and expected returns.